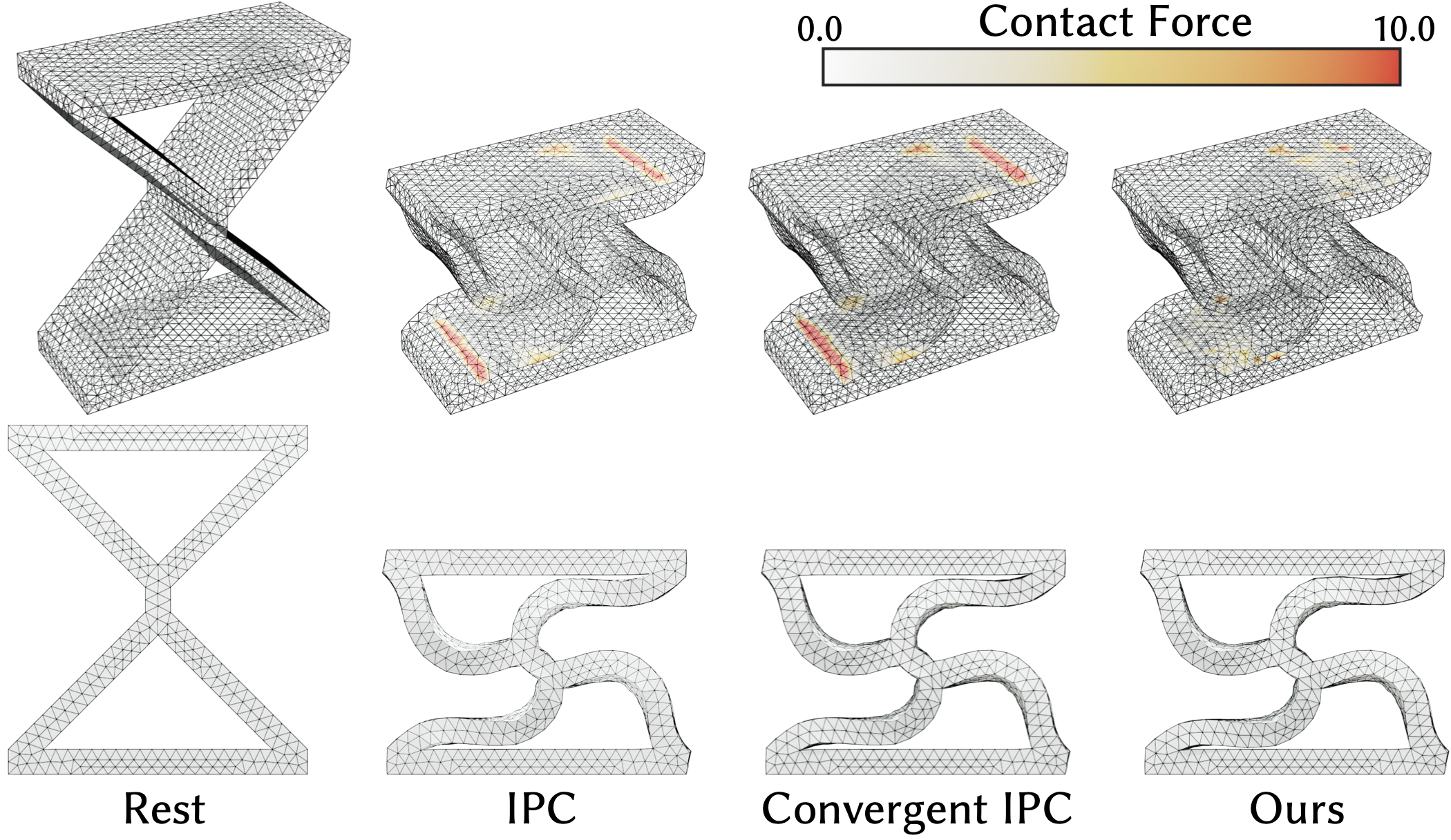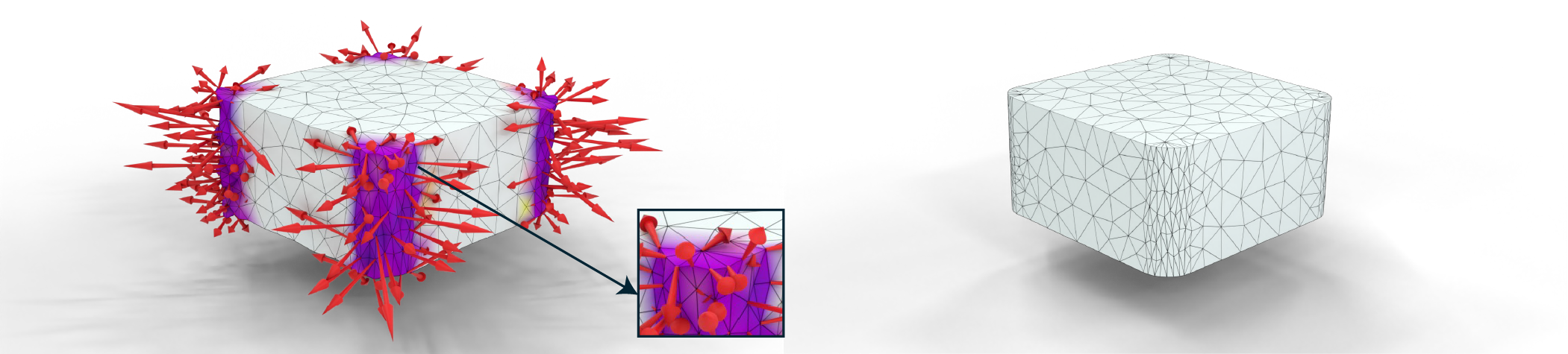
Our method (right) elliminates the spurious collision forces in IPC (left).

Our method (right) elliminates the spurious collision forces in IPC (left).
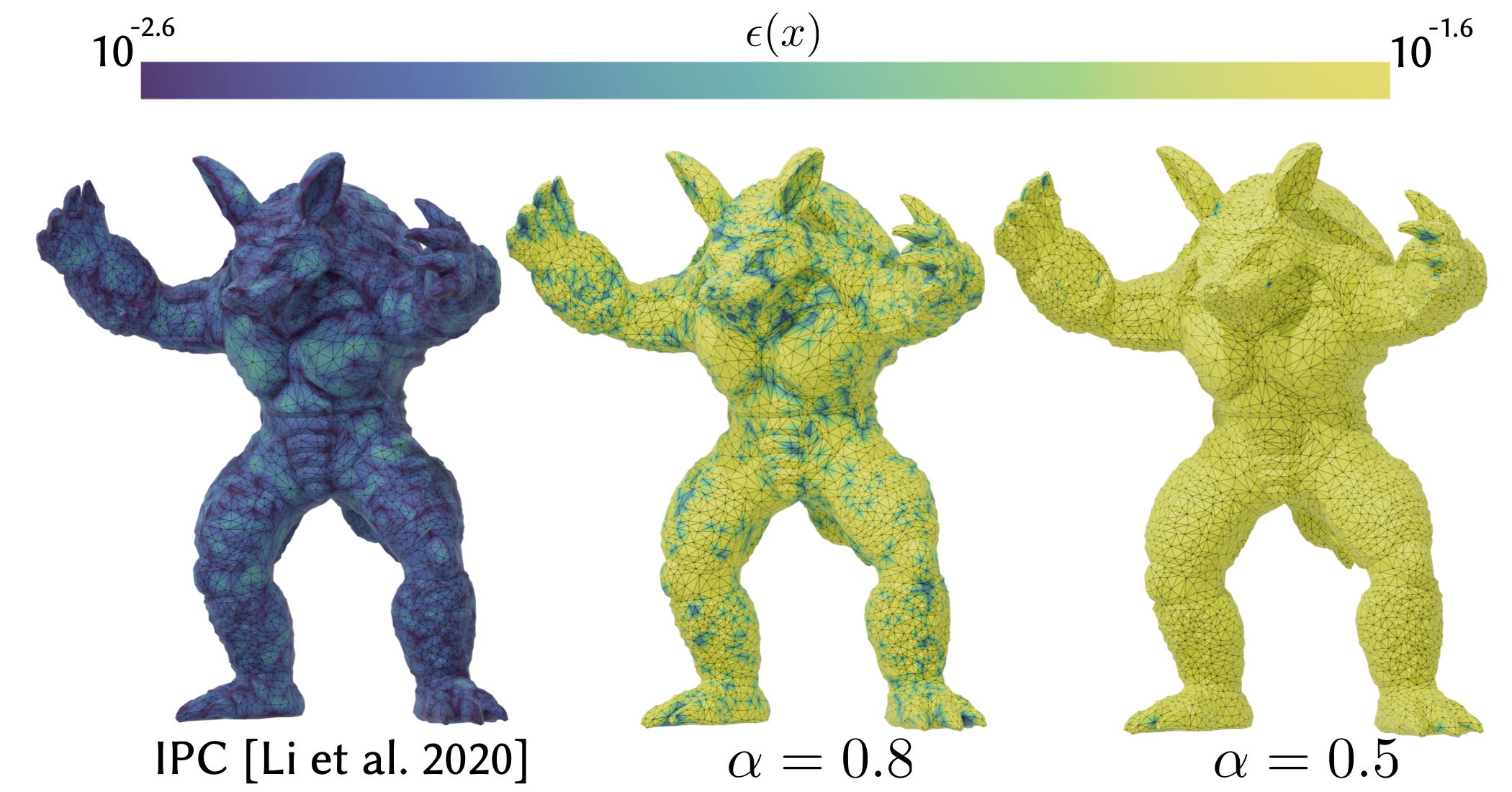
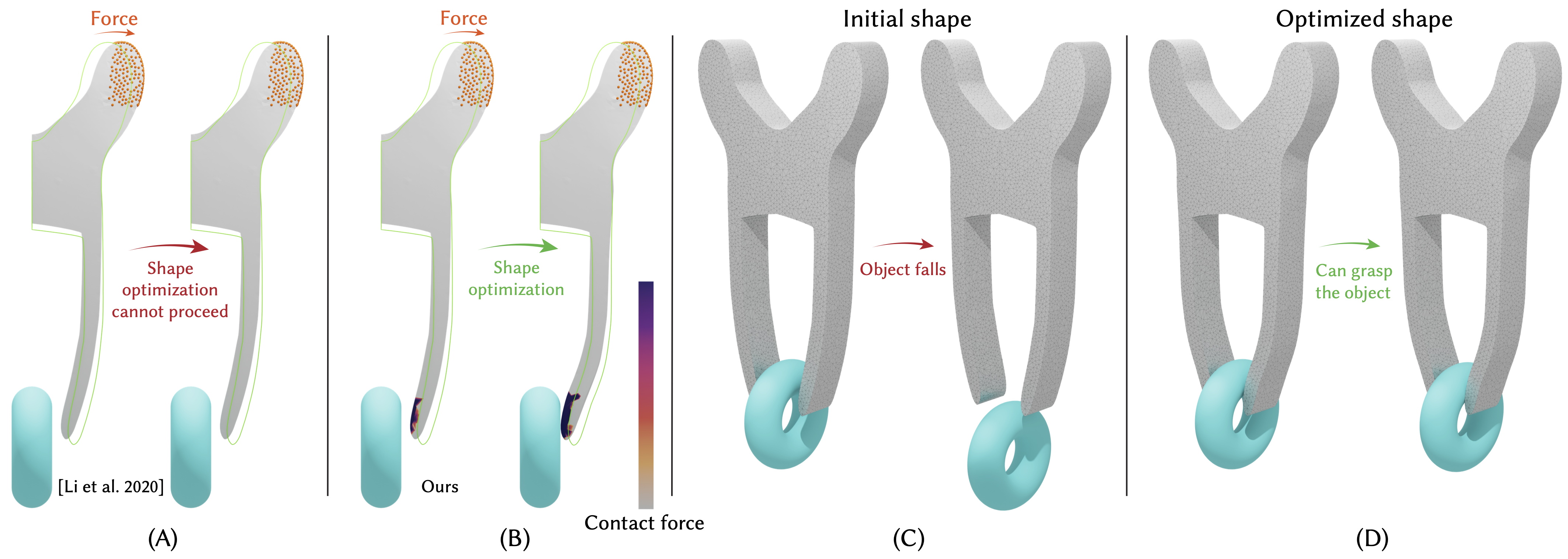
Barrier potentials gained popularity as a means for robust contact handling in physical modeling and for modeling self-avoiding shapes. The key to the success of these approaches is adherence to geometric constraints, i.e., avoiding intersections, which are the cause of most robustness problems in complex deformation simulation with contact. However, existing barrier-potential methods may lead to spurious forces and imperfect satisfaction of the geometric constraints. They may have strong resolution dependence, requiring careful adaptation of the potential parameters to the object discretizations.
We present a systematic derivation of a continuum potential defined for smooth and piecewise smooth surfaces, starting from identifying a set of natural requirements for contact potentials, including the barrier property, locality, differentiable dependence on shape, and absence of forces in rest configurations. Our potential is formulated independently of surface discretization and addresses the shortcomings of existing potential-based methods while retaining their advantages.
We present a discretization of our potential that is a drop-in replacement for the potential used in IPC, and compare its behavior to other potential formulations, demonstrating that it has the expected behavior. The presented formulation connects existing barrier approaches, as all recent existing methods can be viewed as a variation of the presented potential, and lays a foundation for developing alternative (e.g., higher-order) versions.